Pedro the Pi Rate Panda

Introduction

My AP Calculus Class was supposed to do a "Pedro the Pi Rate Panda Project", but as the concept of our online assignment became broader, it was quickly replaced by the Developing Expert Voices Project. Here is the beginning of the Pedro the Pi Rate Panda Project, which I had composed and completed. I thought it would have been a great waste of time and effort if it was not incorporated into my DEV Project, and so that's exactly what I did. I have added a few more questions, and a "reflection" part after each question to satisfy the requirements in our rubric. Well, please enjoy and have a great day!



It was one of those days when the sun’s rays seemed perfect. Birds were chirping, the trees mildly swaying, and the grass beneath looked greener than it had ever been. It stretched miles and miles, broken here and there by bunched up flowers of all kinds. Thousands of colours before the eyes, and in normal days it would look chaotic. But this was a different day.
It didn't change, Pedro said to himself.
He left the Hugwarts Islands 10 years ago. Pedro tried to convince himself that he'd go search for his father, who left when he was still little and cute. In truth, Pedro wasn’t even half-concerned about his father. He wanted to change his purposeless and mundane life, to one full of excitement. And so Pedro left. After all, he was a teenager, and every living creature, save a few, had thoughts like his. An ordinary being would not act on his thoughts, but Pedro was not like that at all. He was one of those few who knew for a fact that thoughts, valuable as they are, aren't worth much unless coupled with action. This time, however, the rolling green meadows with flowers and tress, the butterflies and bees were calling him. He didn’t know why, but it almost felt like something was dragging him. Daydreaming about the sight before him, Pedro suddenly tripped and fell on his face.

He stayed there, face down, for a few seconds, when he heard someone giggle not far off. The noise stopped abruptly. Whoever it was has been following Pedro for a while, and the panda knew of it. He decided not to confront the follower just yet.

As he stood, Pedro saw someone coming. The melodic chirping of birds, swaying trees, flowing water, were ignored. Heart pounding. Dub dub. Dub dub. Pedro knew who it was. Hisoka. He was one of only about ten white tigers left in the world, adored and respected by everyone despite his age. Every creature knows of someone who, for some unknown reason, seemed to be a magnet to others.
Pedro didn’t know what to do. He was arguing whether to hide from his childhood friend, or face him. Sure, they were best friends, born on the exact day, growing up together, eating on the same dishes, but Pedro left without notice. He thought of the short note he left. It read, “I will be gone for some time. I’m looking for dad.”
That was stupid. Pedro thought, pounding his head with enormous paws. STUPID!
Half an hour after he left his house, Pedro heard the most terrifying cry in his life. The roaring was as loud and as harsh as a tiger can make it. It sounded of glass breaking right beside the ears, magnified by a hundred, longer by a hundred. Pedro knew it was from Hisoka, and it seemed to say, “and I thought we were friends…” Most would find that cry too dramatic, but what could be expected of Hisoka? Not a day passed when the panda-tiger duo didn't spend time with each other. Not a day passed when Pedro didn't poke fun on Fishy, the cute little turtle, for his one shorter leg thing; not a day passed when he missed the opportunity to prank big-old-CowCow the cheesemaker, while Hisoka stayed behind to take the blame and fix the mess.

The majestic figure of the white tiger appeared closer and closer to Pedro. Then it stopped. About fifty metres away from Pedro, Hisoka stared, dumbfounded. He stood with confidence, but that confidence, it seemed, was shaken.
“So you’re back,” Hisoka said.
“I… I’m sorry,” answered Pedro, looking down.
Hisoka started to walk towards Pedro, gliding on green grass with a King's grace, until the two were face to face.
“Pedro,” the white tiger said, “why are you here?”
“I didn’t know better, Hisoka.. I really didn’t… I’m sorry… don’t make me cry…” All of a sudden, Pedro was hit on the head with massive paws, falling flat on his face.
“What the heck was that for?!?” then Pedro, once again, was beaten down to the grass that before he loved and now hated.
“I’ll make you regret the second your father laid eyes on your mother!” said Hisoka. “You should not have left your house you dimwitted dodo head!” All that was regal about the tiger was gone. “You left your mother, Mrs Regina Orangina Lupin III, alone!” The beatings kept coming. Hisoka rambled on, anger replacing the faint joy that was in his eyes when he first saw Pedro. “You left ME alone you…” Anger turned to longing, like that of a brother to a brother. He started sobbing. The assault stopped. A pause went on for seemingly forever, when Hisoka said, “I missed you Pedro, that’s all…” Hisoka's little speech was interrupted when, out of nowhere, tiny hands grabbed his tail and he was spun around like a ball of yarn. It was the follower.
No one could have believed such a small thing could even lift an apple, but there the creature was, acting like a cowboy with his ropes. It threw Hisoka into the air, far away, nearly out of sight. Thud. Hisoka fell. Pedro got up, in shock, and even more so when he saw how far Hisoka had gotten.
“HI!” said the creature. “My name’s Kuro Kuro, and I want to be your…”
“What did you just do?! Oh man… Hisoka… I’ll be there don’t worry…”
And with that, Pedro ran towards where his friend landed.
“…friend…” Kuro Kuro continued, nearly without spirit as a deer’s carcass.




Pedro ran after Hisoka. When he caught up, he reached for the tiger and helped him up. Blasted… thing.
“What was that, Pedro?” asked the tiger, all hostility towards the panda now gone.
“I have no idea. MY GOSH I’m so mad!”
“No matter, Pedro. We have more pressing things to worry about.” The look of wisdom was back. There were those who tried to be wise, and those who just were, and one can never be taken for the other. Hisoka was a prime example of the latter.
“Is there anything wrong, Hisoka?” Frowns formed on Pedro’s face.
“Well, about an hour ago, five large humans, dressed in fancy suits, came to your house. They were asking for you, and Mrs. Regina Orangina Lupin III said she did not know of anyone named Pedro.” Pedro’s frown deepened. He was concerned about those uninvited guests, but was more troubled by what his mother apparently said.
“In any case,” Hisoka continued, “you should leave. They brought a declaration from Queen Hopra Winfrey, the Mistress of All The Hugwarts Islands, demanding anyone who knows anything about you to report to her guards. She wants you, Pedro, and what Hopra wants, Hopra gets.” Hisoka’s tone was almost too cold; too matter of fact.
“What could I possibly have that the Queen would want? I have nothing, Hisoka, none.” Pedro was almost pleading. Other than his escapade, he had done nothing that could even slightly interest Queen Hopra.

Queen Hopra was popular among her subjects. Besides her significant weight loss, she had done many things worth noting. Queen Hopra, whose ancient title included being the Mistress of All The Hugwarts Islands, led her kingdom to prosperity. "The forgotten wart-plagued-hogs place," as it was branded before, was transformed into the center of commerce and culture of the world. The Hugwarts Islands was the place to be, the source of popular culture and dictator of what went on in the global theatre. Among so many that Queen Hopra raised from poverty to fame was Tom Hortons. Mr. Hortons was just a regular neurosurgeon, earning three eggs a day, when he was discovered by the Mistress of All the Hugwarts Islands. He would become known as the founder of McStarrybucks, a global fastfood chain/tv station. Hopra was also known for giving away lots of expensive donkeys, the most common transportation in the land. In one of her parades, Queen Hopra was known for giving away a thousand donkeys, pointing at someone randomly and saying, “you get a donkey, you get a donkey, you get a donkey!” Surely enough, those people got donkeys. But that was the peak of her glory. She soon started to gain weight again, and became grumpy. She reinstated slavery, and not long after that, the Queen personally wrote particularly cruel declarations. Soon, Hopra was either extremely loved for what she had been able to do for the Hugwarts Islands, or extremely hated for what she had become.
“I don’t know what they want, Pedro, but as soon as those humans left, I went to search for you, and there we met at…” Hisoka’s voice drifted in Pedro’s head. None else seemed more pressing than that a grumpy queen, Cruella Devil incarnate, was hunting for him. He cut his friend off, “Hisoka, we must go to my house. I need to know what’s going on. Well, and say hi to my mom too.”

As they reached the house, an old panda opened the door, who appeared to be in horror, gasping, sunken eyes staring straight ahead at Pedro. Mrs. Regina Orangina Lupin III was, at most half of what she was, before Pedro left ten years ago. Tears started to well in her eyes, when she was grabbed by her son and was hugged with enormous arms.
“Forgive me, mummy Mrs. Regina Orangina Lupin III.” Pedro’s voice was as steady as a rock. My gosh, she’s thin. “I’m happy you’re alright,” Pedro continued, almost mechanically.
“Well,” Mrs. Regina Orangina Lupin III began, with the grace of a princess that she’s always had. “I must cut our reunion short. You have to leave this town, this country even, NOW!”
“But mum..”, Pedro was taken aback by the sudden outburst of emotion.
“I said now!” Her eyes were even better at giving commands than her words. “I know there are people watching this house at this very moment. Those five that visited this afternoon are still here. I know this, Pedro, trust me. LEAVE! NOW!”
“MOM! WHAT ARE THEY AFTER?! COULD YOU PLEASE JUST TELL ME?!”
“Pedro, that necklace your father gave you….” when all of a sudden, the front doors were kicked open, splitting into countless shards.
“PEDRO, RUN!” Hisoka said. “I’ll stay here with Mrs. Regina Orangina Lupin III.”
“Hisoka…”
Hisoka shot Pedro a look that made the panda stop. “I was your friend since birth, and even when you left me, we were still friends…”, the eyes seemed to say. “I would gladly face these monsters for you.” All of these were in Hisoka’s eyes. It started to rain.

Pedro ran outside, through the back doors. He ran and ran, trying to go faster. He came within sight of the donkey he used when he went home. Pedro ran even faster, rain on his face, until he reached the donkey. As he hopped on it, he suddenly realized that he forgot his McStarrybucks coupons, so he galloped towards the house. Pandas' cravings for McStarrybucks Whopping Good Frapuccino had to be quenched. About three kilometres away from the house, Pedro stopped. The whole town was on fire. The rain did little to stop the blaze. Pedro was in shock. I’ll make them pay. Patience, Pedro. You must wait. He was scared, but he also well knew there was nothing he could have done. The Queen wants something, and she’s willing to use violence to get it from me. That forces me to believe she should not have it. The necklace dangled from Pedro’s neck, shining despite the rain. He finally decided to push the donkey hard away from the town. Pedro’s stamina was tested. He felt as tired running, as trying to stay on the donkey. He fed his tiring body with anger and determination, and the combination of the two made him keep going. The donkey kept galloping until Pedro felt he was safe. He sighed. My gosh, gladly it's now done.. BOOM!
The donkey stepped on a mine and exploded. Pedro, luckily, survived the blast. From a distance, he can see a battalion of soldiers coming towards him. Leading them was a man on horseback, wearing full knights’ armor, with a helmet that had five coloured feathers sticking out. He was holding something out that Pedro couldn’t quite make out. As they got closer, it seemed clearer. Pedro shivered. He could not believe what he was seeing. The officer was holding out Hisoka’s bodiless head. “Give up, commoner! If you don’t want to be like your friend!”
Pedro just stood where he was, staring. He wore a blank expression. Neither grief, nor anger was on his face, but pure unknowing. It was as if he was just born at that instant, clueless about everything and anything he saw, or heard, or felt. The soldiers came nearer.
Something touched Pedro’s paws. It held Pedro tighter, and all of a sudden, he and the creature were on air, flying, getting away from the soldiers. I will not leave you alone, Kuro Kuro thought. .



Pedro sat on a rock beside a river. They were far away from the soldiers now, even far away from Hugwarts Islands. Tears flowed from Pedro’s eyes. He was completely serene, nothing but the swaying of the trees behind them and the river flowing in front could be heard. He was just staring on a lone red rose on the other side of the river, expressionless, but for the flood of tears from his eyes. He’s been like this for two hours, Kuro Kuro thought.
Seemingly out of nowhere, Pedro said, “Thank you…”
“Kuro Kuro’s the name”
“Thanks, Kuro Kuro.”
Pedro wore a different expression now. Not grief, not anger, but acceptance. His speech was so cold, and so contradictory to how he looked.
“I will have my revenge.”
Clear and simple. Pedro was alone, save the little creature sitting beside him. He was not going to ask for help. It was his dilemma, and he had to solve it. His course was set. The wheels of vengeance have started to turn. The road to retribution began for he who would become known as Pedro the Pi-Rate Panda.

TO BE CONTINUED....


PROBLEM 1:

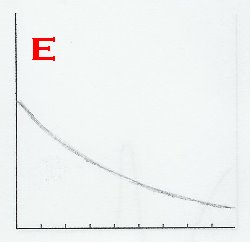
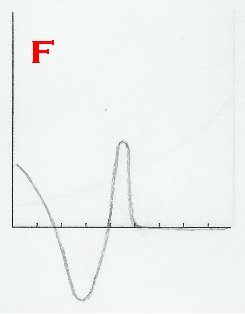
This problem pertains to "Pedro's Escape", as seen in The Revelations chapter of the story, beginning as soon as Pedro leaves the house, and ending when the donkey dies. Given below are six graphs, labeled A-F. Identify Pedro's position-time graph, velocity-time graph, and acceleration-time graph. Justify your answers.

Notes: Assume that pandas and donkeys have tremendous endurance. Their velocities are comparable with each other.










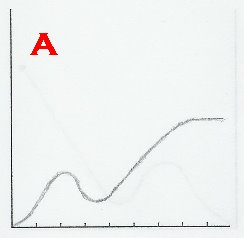
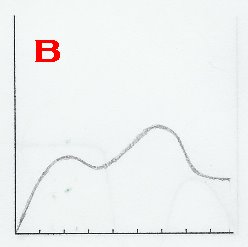
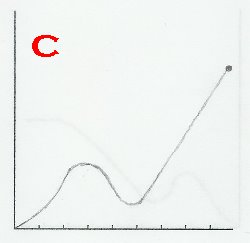
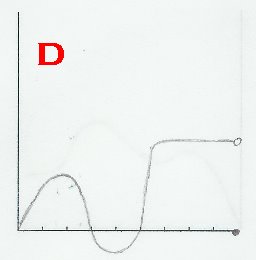
SOLUTION:

Well to start with, we could look at the details of the story and find anything that stands out. For me, it's when the donkey exploded. When this incident occured, Pedro immediately came to a halt, and his velocity dropped to zero. We've dealt with graphs before where, at the end, they gradually plateau (e.g. figure 1), but for this problem, it shouldn't. Pedro and the donkey didn't slow down then screeched to a halt; the donkey just went boom in the middle of its gallop! So, graphs A, B, D or F can't be the position-time graph. This leaves C and E. Well, if you take a look at E, it's decreasing throughout. We know that Pedro starts the journey off by going in the positive direction, goes back, and dashes away on a positive position again, so E can't be it. Therefore, C is the position-time graph.

.

It's been said that Pedro just abruptly stops, right? That means that his velocity just dropped to zero, and A, B, C or E can't be the velocity-time graph. Well, if you take a look at graph D, at the end of it is a removable discontinuity. The output just suddenly became zero, and that's promising. If you take a look at graph F, it appears to just drop to zero, but if it is a vertical line, then it wouldn't even be a function. So, graph F isn't the velocity-time graph, but D.

.

Now comes the actual calculus solutions. So far, we've been able to determine the parent and first derivative graphs simply through common sense. Well, we'll get to the core of derivatives shortly.

.

We learned that a derivative is rate of change, or the slope of a tangent line on a given graph. If we don't, don't, don't forget that a derivative is a slope, then we should be fine.

.

Let's confirm our answers above first (f is graph C, f' is graph D). Well, at the minimum or maximum of C, there should be a root on D, right? If you take a look at the graphs, this is indeed the case. Also, Where C is decreasing, D should be below the x-axis, and where C is increasing, D should be above the x-axis, and that is true for the graphs.

.

When it comes to the second-derivative graph, we can first observe the slopes of D. Where there are minima or maxima in D, there should be a root in f", right? Well, which among A,B,E and F fit this? Seems like only F fits this. Assuming that F is the second derivative graph, wherever it has a root, there should be a point of inflection on C. Wherever C is concave up, F must be below the x-axis, and wherever C is concave down, F must be below the x-axis. If we check, we'll see that what I've described does occur for the two graphs. Therefore, F is the acceleration-time graph.

REFLECTION ON QUESTION 1:

I rather like these graphing questions, because it requires logic and complete understanding of what's going on. At the same time we learned this lesson in Calculus, I was also taking Physics 40S; and velocity, distance and acceleration were among the topics taught. Being a part of Mr. Kuropatwa's class, I was glad about being able to apply what I learned in Calculus to another subject. Honestly, I saw velocity, distance and acceleration questions in a different light, and thought to myself, "Ahh, now that makes more sense..". I am very happy with my understanding of the relationships between parent function graphs, first derivative graphs and second derivative graphs, therefore used them for my DEV Project.

PROBLEM 2:

The function f(x) = √(x+4) is locally linear at x = 0.

(a) Find the tangent line equation to the graph of f at x = o.

(b) Using the tangent line, estimate the integral .

SOLUTION:

(a) Using a calculator, we can determine that the derivative of f at x = o is 0.5, therefore m = 0.5000.

We are trying to come up with an equation for a line, therefore we must find the components m and b in y = mx + b. We plug in zero (0) to f(x) first, to see where the y-intercept is. Since we know what m is, and we evaluated what y is, we find out that the tangent line equation at x = 0 is y = 0.5000x + 2.

(b) The graph of y = 0.5000x + 2 looks like this:

We can use the left hand sum or right hand sum to approximate , or do both, add them together and divide by two for a closer approximation.

LH SUM = 2.0
RH SUM = 2.5

LH SUM + RH SUM = 4.5

4.5 / 2 = 2.25

REFLECTION ON QUESTION 2:

This is a very interesting question for me, because it can easily be applied in real life. So long as we know basic measurement-taking skills, we can use this procedure to figure out the velocity at which our car is going or anything of the sort. Of course, however, who would do that haha ;-). At its core, this is a simple approximation question, and although these are relatively easy to do, they, once again, need to show some understanding. It can't be purely mechanical. This is one of the best understood topics throughout the year for me, and so I used it for my DEV Project.

PROBLEM 3:

Imagine a line segment from the point (0, 5) to (10, 0). Revolve this line on the x-axis, and you’d get a cone, as seen in the diagram below.

SOLUTION:

To find the volume, we follow these three steps:

(1) Find the function that represents the radius.
(2) Replace "r" with this function in the "volume equation" we come up with.
(3) Integrate over the interval.

REFLECTION ON QUESTION 3:

This is one of the advanced topics we learned in the year. If a grade 12 Pre-Calculus student looked at it, they wouldn't know what's going on. I used this problem because it shows the depth of learning we had in class. Our learning was at another level, above high school level, and I thought it would be appropriate to use it for my DEV Project.

OVERALL, the DEV Project was helpful because it helped us really and truly value learning. We understand the effort that goes into planning classes and coming up with questions. Learning is a two-way street; both parties, the teachers and the students, must interact with one another. This DEV Project might well be one of the most difficult projects in my high school career, but also one of the most valuable.